What's in for you?

I'm distilling the essence of this sorting algorithm. Rest assured, I've left no stone unturned. By the time you finish reading this blog, you'll not only grasp the concept thoroughly but be ready to explain it effortlessly to anyone!

What sets sorting algorithms apart?

Every sorting algorithm distinguishes itself through the unique steps it takes. The specific actions undertaken in each steps contribute to the distinctive nature that sets each algorithm apart from the others. Now Let's Hop into the main algorithm for which i have written this blog!

Bubble Sort

Bubble Sort by other names is also called as Comparison Sort , Sinking Sort or Exchange Sort. What are we basically doing in Bubble Sort?

We're just letting bubbles rise to give our fish a breather. Just kidding, no aquatic adventures, just sorting algorithms at work! Here in every steps we are comparing adjacent elements!

To ensure a clear understanding, I'll be breaking down the explanation into two parts for a more comprehensive grasp.

What are we doing?

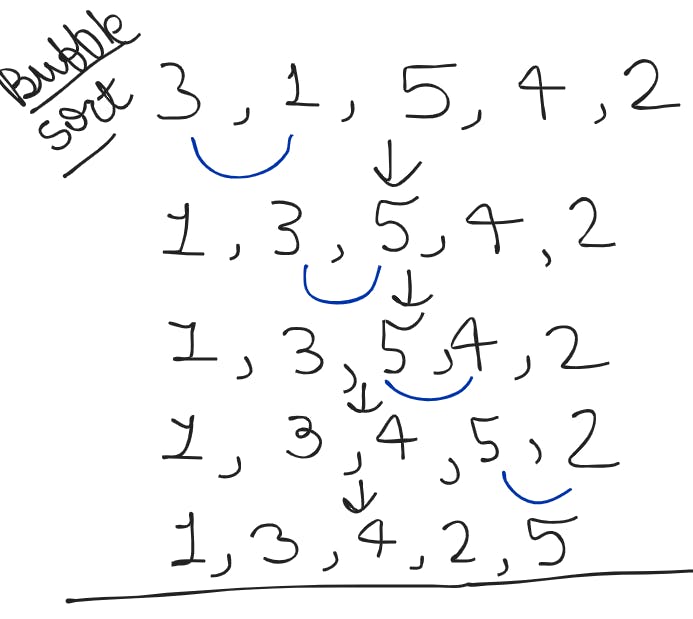
As you can clearly see in the image down there this is a step in which in each operation we are comparing adjacent elements and you can clearly see after iterating the whole array (passing array) we have the largest element right in the last index!

Why are we doing?

Okay I mean we are comparing adjacent elements But Why? :) You can now clearly see with the first pass through the array the largest element came to the end! Similarly in the second pass through the array the second largest elements comes to the second last end. Similarly if i do the third pass the third largest element will be at the third index from the last and this goes on till the array is sorted!

So the Reason is now Clear :)

With Every Step/Pass the Remaining Largest Element is coming at the end.

Now Let's Go in Space

Congratulations, space explorer! But hold on—Google hasn't extended its offices to Mars yet. Time to zoom back to Earth 🌎 for some algorithmic concepts!

Space Complexity
Time Complexity

Space Complexity

The Space Complexity of Bubble Sort is O(1) that is Constant Space Complexity , It means No extra space required as we are not creating any arrays a.k.a in-place sorting algorithm.

Time Complexity

We often explore two cases when talking about time complexity. Let's take a closer look at them.

Best Case - O(N) ⇒ This happens when array is sorted.

Worst Case - O(N²) ⇒ This happens when array is sorted in opposite like if an array is given in descending order and you have to sort it in ascending order.

Let's visualise 'N' ⇒ N as the number of comparisons.

For example, if your array size is 100:

Best Case: Only 100 comparisons needed.
Worst Case: Requiring (100)² comparisons, which equals 10000 comparisons.

Now, if the array size is 50:

Best Case: Just 50 comparisons.
Worst Case: Requiring (50)² comparisons, totalling 2500 comparisons.

In essence, TIME COMPLEXITY reflects how the time grows as the input size increases.

You can clearly see :

As the size of array is growing the number of comparisons is also growing! to understand it better let's deep into these cases more:

Best Case

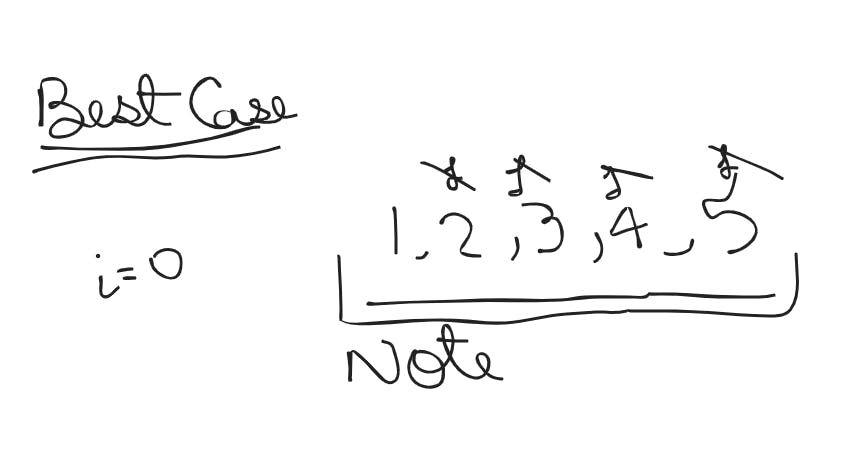
Note ⇒ If 'j' never swaps for a value of 'i' (during the 'i'th pass), it indicates the array is already sorted. Consequently, you can terminate the program.

In the Best Case scenario, the number of comparisons is generally N - 1, but in Time Complexity (TC), constants are disregarded. Therefore:

Best Case ⇒ Comparisons ⇒ N, as we focus on the mathematical relationship rather than the precise time.

Worst Case

To enhance the understanding of this case, I've included images that meticulously illustrate every iteration, showcasing each step in detail. Pay close attention to key aspects, such as the number of comparisons made in each pass. These visuals will provide a comprehensive insight into the workings of the algorithm.

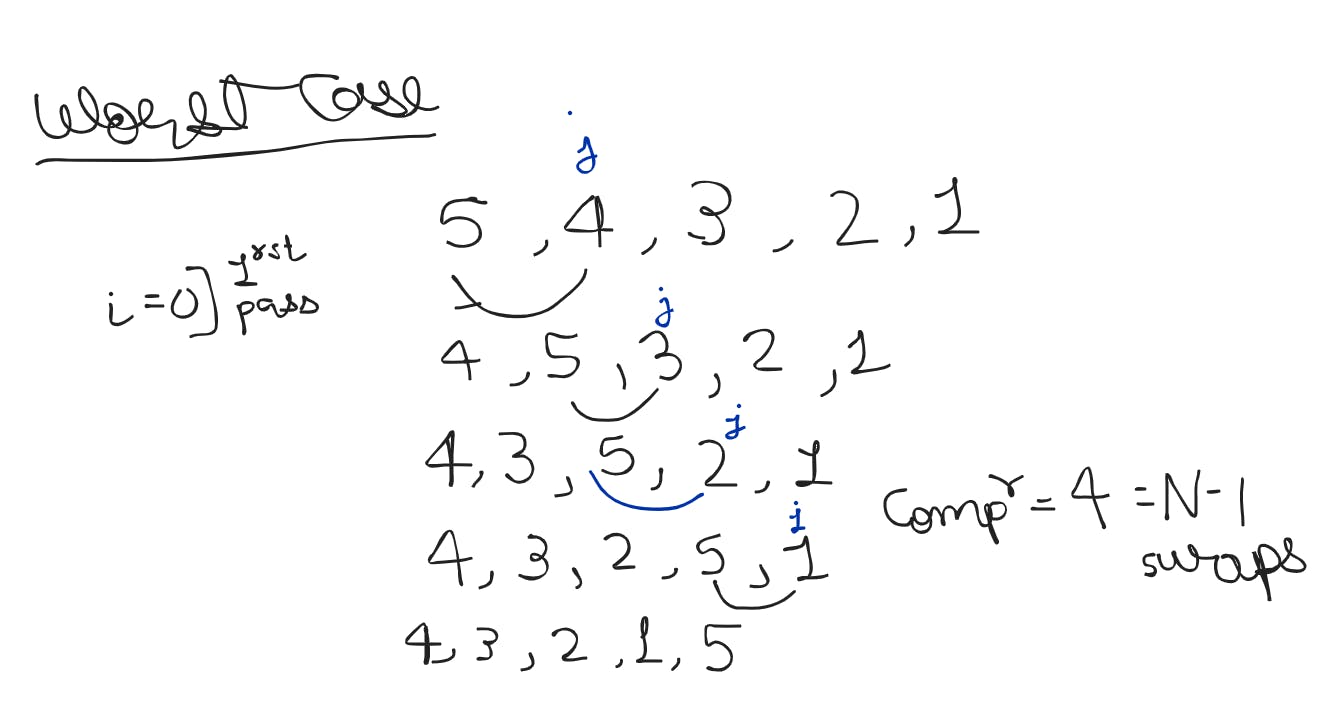
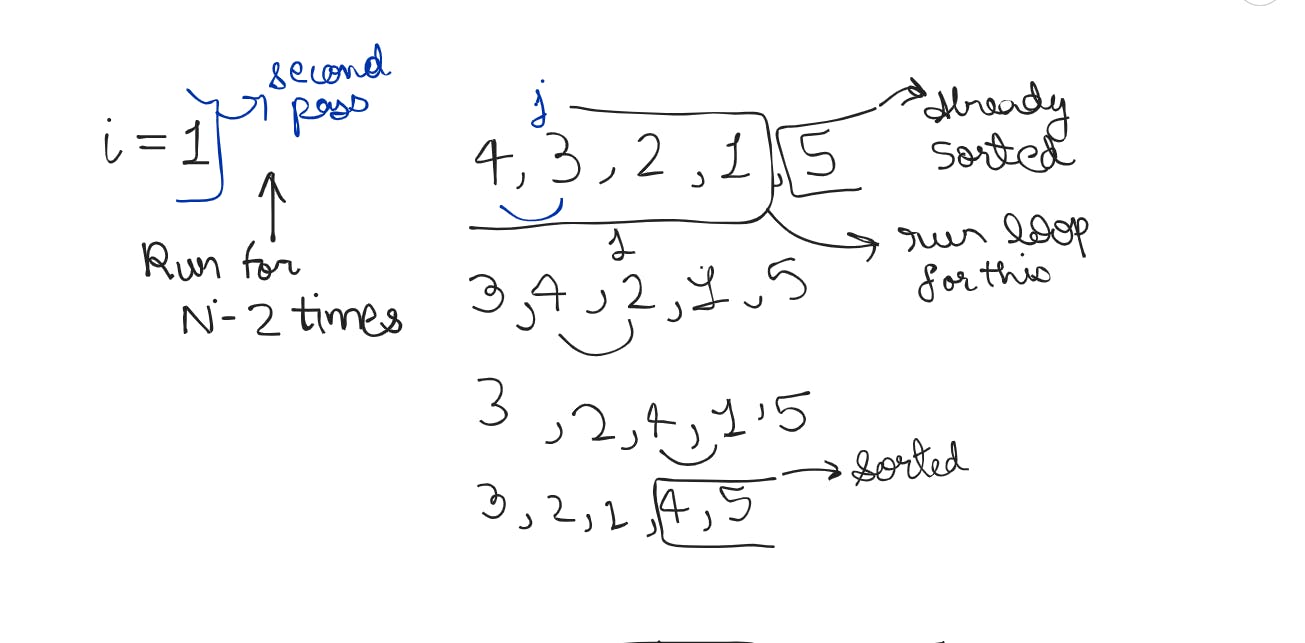
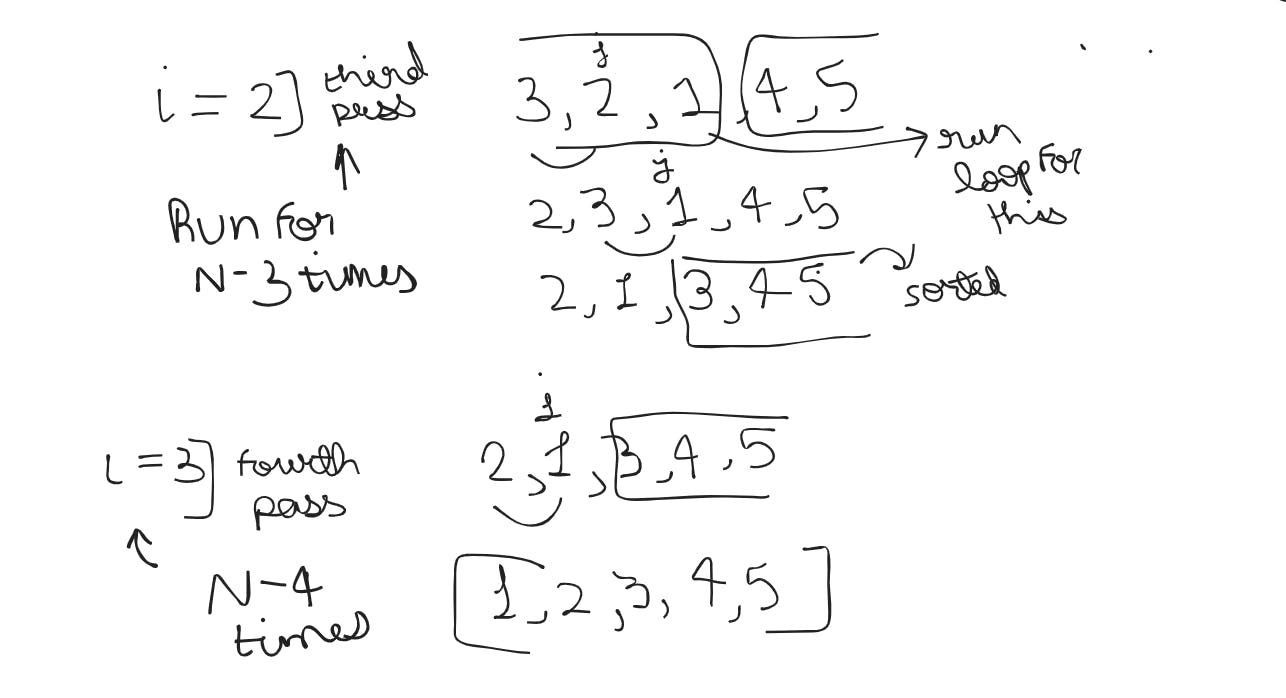
So Internal loop ( j ) is going to run till ⇒ n - i - 1

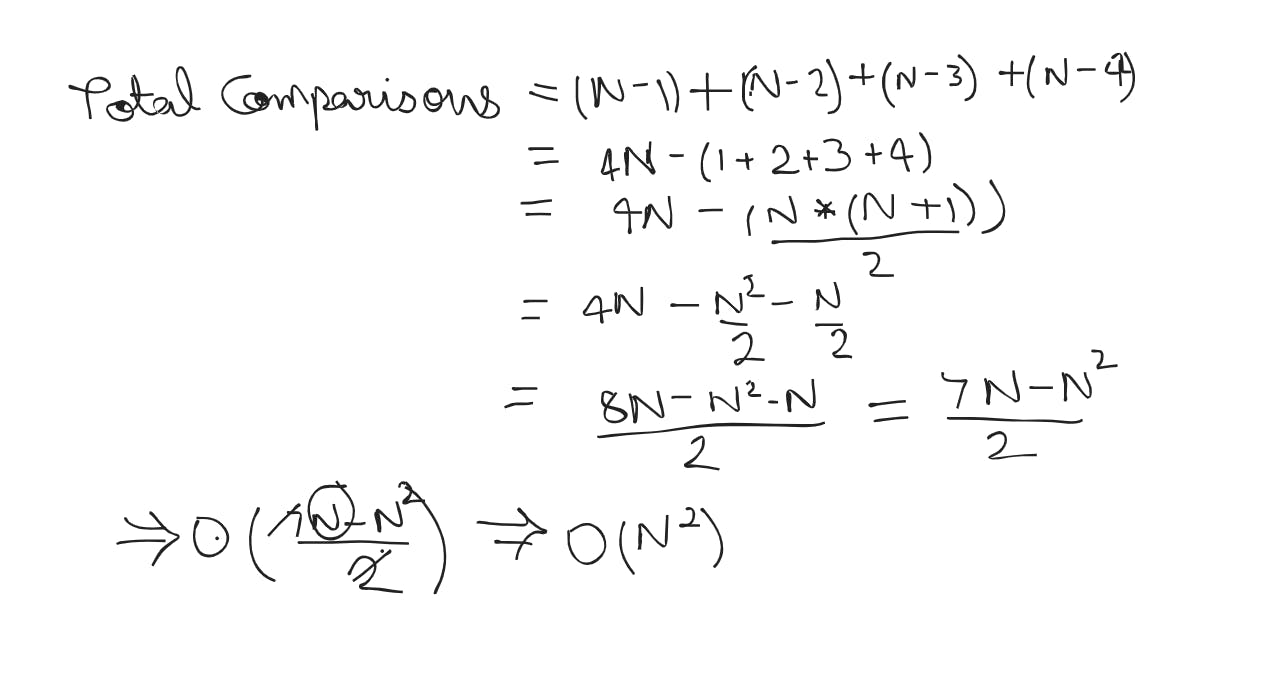
Here, you might be curious about why I cancelled out all the constants and 'N' in the calculation. When determining time complexity, we focus on the dominating terms and eliminate less impactful factors and constants. It allows us to analyse the fundamental growth of the algorithm's performance without getting bogged down by specific numerical values.

Here's the code of Bubble Sort I have done it in java -

public class Main{
    public static void main(String args[])
    {
        int arr[] = {5,4,3,2,1};
        bubble(arr);
        System.out.println(Arrays.toString(arr));// output: {1,2,3,4,5}
    }

    static void bubble(int arr[]){
        boolean swapped = false;
        // run the steps n-1 times
        for(int i = 0; i<arr.length; i++){
            //for each step, max item will come at the last respective index
            for(int j=1; j <= arr.length - i - 1; j++){
                //swap if the item is smaller than the previous item
                if(arr[j] < arr[j-1]){
                    //swap
                    int temp = arr[j];
                    arr[j] = arr[j-1];
                    arr[j-1] = temp;
                    boolean swapped = true;
                }
            }

        // if you do not stop swap for a particular value of i, it means the array 
        // is sorted hence stop the program
            if(!swapped){
                break;
            }
        }
    }
}

Great job if you stayed till the end! That's all, and we've covered every aspect of this algorithm!

There We Are! That is what is Bubble Sort :)

Want to learn more? Stay tuned for my next blog! If you found this helpful, share it with others. Follow me for more interesting stuff.

Connect with me on Twitter Linkedln GitHub!

Thank you for Reading :)

Divv Saxena