What's in for you?

I'm distilling the essence of this sorting algorithm. Rest assured, I've left no stone unturned. By the time you finish reading this blog, you'll not only grasp the concept thoroughly but be ready to explain it effortlessly to anyone!

Selection Sort

The basic idea is to iteratively select the largest (or smallest) element from the unsorted part and place it in its correct position in the sorted part. This process is repeated until the entire array is sorted.

Two Approaches:

Approach 1: Selecting the Largest Element

In each iteration, find the largest element in the unsorted part and place it at the end of the sorted part.

Approach 2: Selecting the Smallest Element

In each iteration, find the smallest element in the unsorted part and place it at the beginning of the sorted part.

Approach

To provide a clearer explanation of the concept, let's delve into a specific example. Imagine you have an array, and you're applying the Selection Sort algorithm with the approach of selecting the largest element. Let's refer the image down below to illustrate the process:

you can clearly see in the image for i = 0 the first thing that is happening it is identifying the maximum element in the array and then swapping of that maximum element is taking place!

The position of the last index also changes in a predictable way After analysing the pattern. Change occurs N - i - 1 times in each step, where N is the total number of elements in an array and i is the current iteration. Imagine starting with the whole array unsorted. During each iteration, the algorithm finds the maximum element in the unsorted part and swaps it with the last element in that section.

This swapping, happening between the maximum element and the last index of the current step, positions the largest elements correctly. The pattern of N - i - 1 reveals a clear and organized progression in sorting the array.

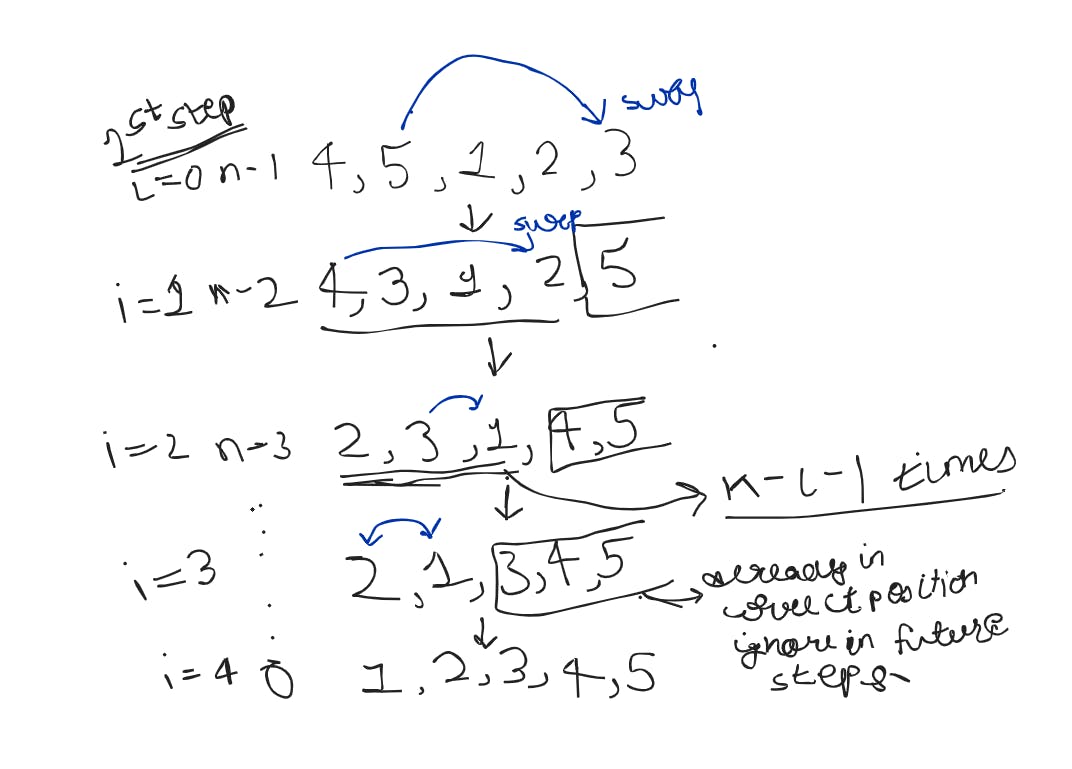
Time Complexity

Worst Case ⇒ O(N²)

Best Case ⇒O(N²) because in any case it is finding the maximum element in the array.

Stability ⇒ It is not Stable Sorting Algorithm

You might be wondering how we get to the conclusion of getting the complexity as O(N²) It is because of this equation that we have formed!

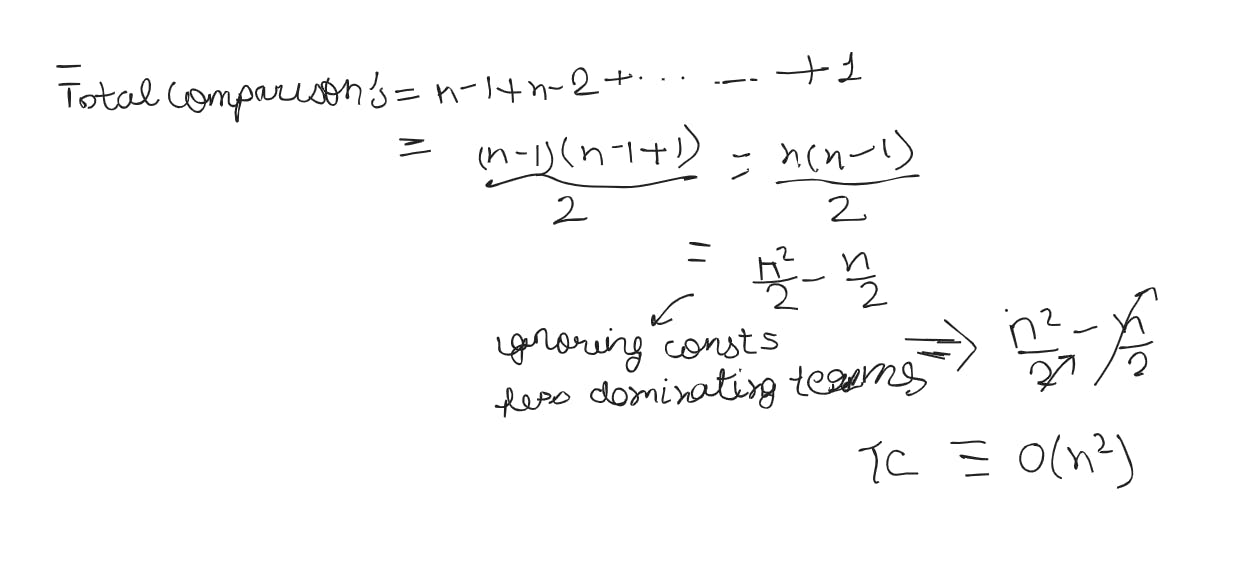
Use Case

It performs well on small lists / arrays.

Let's Hop in Some Code

I have used Java to explain selection sort but if you are used to code in different language then no worries just understand the process and then you will be able to implement it in any language!

first find the maximum element in the whole array
then when the loop runs again find the maximum end term in the remaining array
at every point it’s actually running the loop (n - i - 1)th times , you can run the loop till N also but why to compare some elements if they are at the correct position!

  import java.util.Arrays;

  public class bubblesort{
      public static void main(String args[])
      {
          int arr[] = {5,4,3,2,1};
          selectionsort(arr); 
          System.out.println(Arrays.toString(arr));// Output => {1,2,3,4,5}
      }

      static void selectionsort(int arr[]){
          // basically i will swap the last element with the max element present in the array
          for(int i=0; i<arr.length; i++){
              //find the max item in the remaining array and swap with correct index
              int last = arr.length - i -1;
              int maxIndex = getMaxIndex(arr, 0 , last);

              swap(arr, maxIndex, last);
          }
      }

       static int getMaxIndex(int[] arr, int start, int end) {
          int max = start;

          for(int i = start ; i<=end ; i++){
              if(arr[max] < arr[i]){
                  max = i;
              }
          }

          return max;
      }

      static void swap(int arr[], int first , int second){
          int temp = arr[first];
          arr[first] = arr[second];
          arr[second] = temp;
      }
      }
  }

Great job if you stayed till the end! That's all, and we've covered every aspect of this algorithm!

There We Are! That is what is Selection Sort :)

Want to learn more? Stay tuned for my next blog! If you found this helpful, share it with others. Follow me for more interesting stuff.

Connect with me on Twitter Linkedln GitHub!

Thank you for Reading :)

Divv Saxena